【人気ダウンロード！】 ��角形 内角 求め 方 144993-三角形 内角 求め方

 正三角形の面積の求め方がわかる3ステップ がしかし、だ。 公式をおぼえると便利だけど、 忘れた時に悲惨なことになる。 頭真っ白ってやつさ。 今日はそんなときのために、 正三角形の面積の求め方を3ステップで伝授しよう。 例として、 こんにちは、ウチダです。 今日は、中学2年生で習う 「多角形・正多角形の角度」 について、まずは多角形の内角の和・外角の和を考察し、次に正多角形の一つの内角・外角の求め方を考察します。 証明や練習問題なども扱っていますので、ぜひご覧ください こんにちは、ウチダです。 今日は数学a「図形の性質」で習う 「三角形の内心」 について、性質の証明や基本的な使い方(角の二等分線と比)、座標の求め方や位置ベクトル表示などをわかりやすく解説していきたいと思います。 外心に関する記事と内容がか

高校数学a 三角形の内角 外角の二等分線と辺の比の関係とその証明 受験の月

三角形 内角 求め方

三角形 内角 求め方- この記事では、三角形の面積を求める公式をまとめて紹介していきます。 問題に応じた公式の使い分け方もわかりやすく説明しますので、ぜひ参考にしてくださいね！ 目次三角形の面積の公式一覧1 基本公式（底辺 × 高さ ÷ 平行四辺形の面積は、 「面積 底辺 高さ」 「 面 積 = 底 辺 × 高 さ 」 で求められます。 たとえば、「底辺 4 c m ,高さ 3 c m の平行四辺形」の面積は 4 × 3 = 12 c m 2 となります。 これは、平行四辺形の右端の直角三角形を切り取って左側に移すと 「たて 3 c m

内角の和 算数用語集

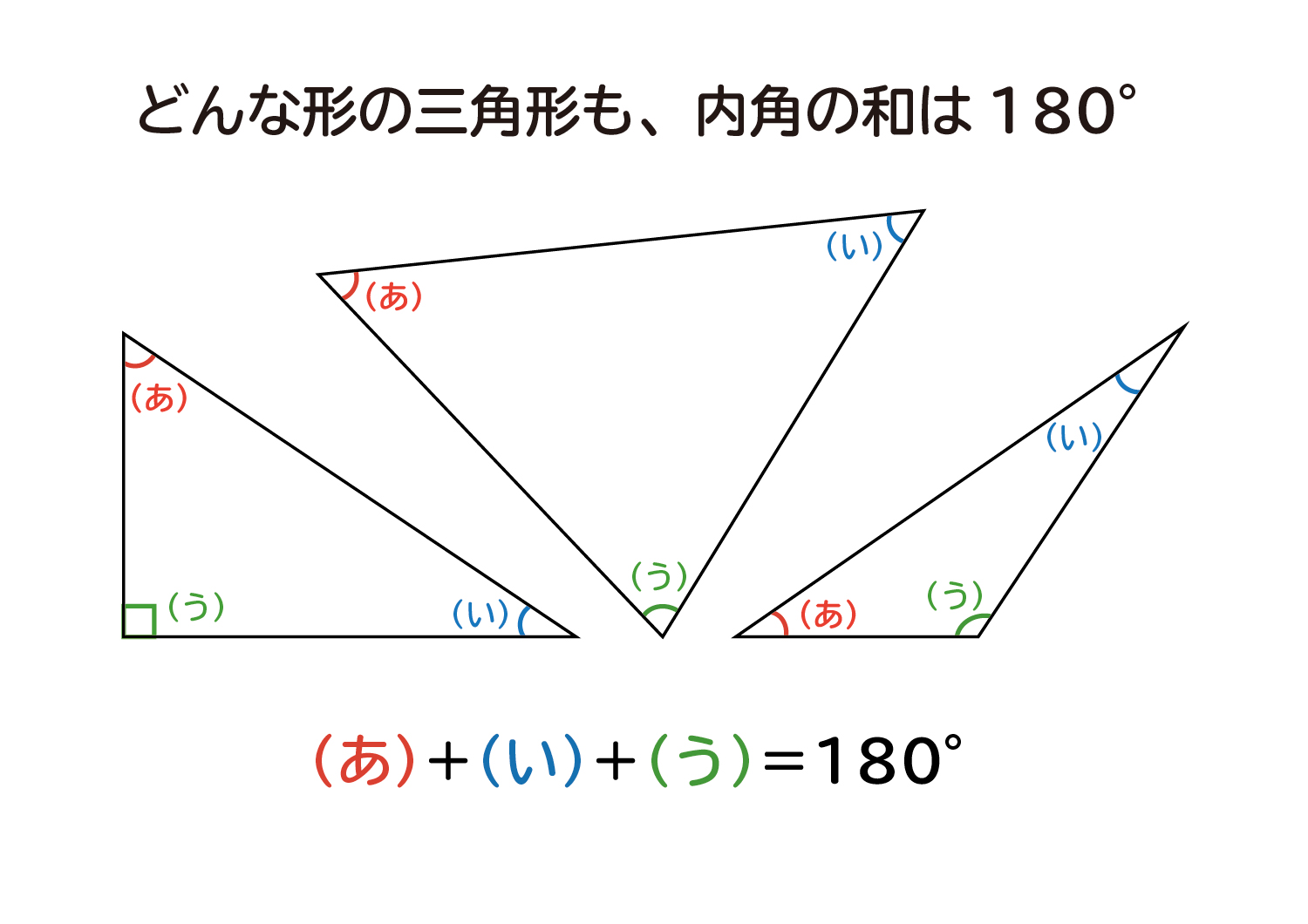
⑤ 内接円の半径・外接円の半径を使った公式 ① 底辺×高さ÷2 上図のような三角形 A B C があったとき、この三角形の面積は 「三角形の面積 底辺 高さ 」 「 三 角 形 の 面 積 = 底 辺 × 高 さ ÷ 2 」 で求められます。 たとえば、「底辺 9 c m 高さ 6 c m の三角形」の面積は 9 × 6 ÷ 2 = 27 c m 2 となります。 なぜ 底辺 高さ 底 辺 × 高 さ ÷ 2 で求まるのかについては 「三角形の面積の求め方。 なぜ底三角形（さんかくけい、さんかっけい、拉 triangulum, 独 Dreieck, 英, 仏 triangle, (古風) trigon）は、同一直線上にない3点と、それらを結ぶ3つの線分からなる多角形。 その3点を三角形の頂点、3つの線分を三角形の辺という。第5学年算数 三角形の内角の和を基に四角形の内角の和の求め方を考え，筋道立てて説明す る。 1 単元名 図形の角 2 単元のねらい (1)三角形の内角の和を調べ，どんな三角形でも180°になることを説明することができる。

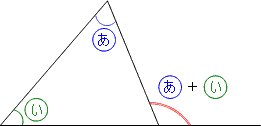
 多角形の内角の和の求め方 多角形の内角の和はどのようにして求めるのかを説明していきます。 ポイントは「 三角形に分ける 」ということです。 前回 三角形の内角の和は\(180^\circ\) であることを確認しています。 三角形の内角の和は180°なので、∠xを求めると 40°75°∠x＝180° → ∠x＝65° 外角と∠xの和は、180°（直線だから）なので、 ∠外角＝180° 65°＝115° ・・・（答え） 外角の求め方② 外角の大きさ＝ ★ を使ってみよう。 ∠外角＝40°75°＝115° ・・・（答え） ほら同じになるでしょ？ ！ だから 三角形の1つの外角は、その隣にない2つの内角の和と等しい 外角は対頂角になっている 内角 (余弦定理) 半径 $1$ の球上にある球面三角形の内角 $\alpha$ は、 によって与えられる。 ここで $a,b,c$ がそれぞれ球面三角形を成す弧の角度である (下の図を参考)。 この式を球面三角形に関する余弦定理という。 球面三角形の内角を中心角(または弧の長さ)から求めることができる。 証明 原点 $O$ を中心とする半径 $1$ の球上にある $3$ 頂点 $A,B,C$ によって構成される球

 今回は、三角形の角度を求める問題を解いていきたいと思います。 三角形の内角の和は180° 三角形の外角の大きさ＝となり合わない2つの内角の和 三角形の角度を求める問題 問題① 問題② 問題③ 問題④ 三角形の角度を求める問題では、対頂角・同位角・錯角の性質や二等辺三角形の性質 （1）三角形の内角の和と外角の定理を利用して、三角形の角の大きさを求めましょう。まず、内角と外角とは何か学んでいきましょう。 三角形の内角の和は、全ての 多角形 たかっけい の角度を求めるときの基礎です。この記事では、三角関数の角度の求め方や変換公式（\\(90^\\circ − \\theta\\) など）についてわかりやすく解説していきます。 三角方程式・三角不等式の計算問題もていねいに説明していくので、この記事を通してぜひ

三角形の内角の和が180 なのはなぜ 小学生に教えるための解説 数学fun

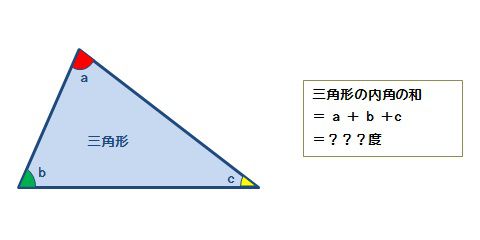
三角形の内角の和 算数の公式覚えてますか

三角形の内角 の でも、内角の和は求め しかしその公式の意味を知っている方は多くないと思います。本ホームページでは公式の意味や公式の導き方を図を使用して分かりやすく説明しています。 この公式考えた人にでも聞くしかないかと－w－ 『このような計算式をつかい、こう計算すれば多角形の内角の和が求められる』っていう風に覚えるしかないので、深く考えないほうがいいですよ。 ちなみに三角形は 180度×（3－2）＝180度。 四角形は 180 30°二等辺三角形とは 30°の内角をもつ二等辺三角形 30°二等辺三角形とは、1つの角度が30°で、それを一端にもつ二辺の長さが等しい二等辺三角形のことです。 面積の基本的な求め方は150°三角形と同じで、三角定規の形から解きます。

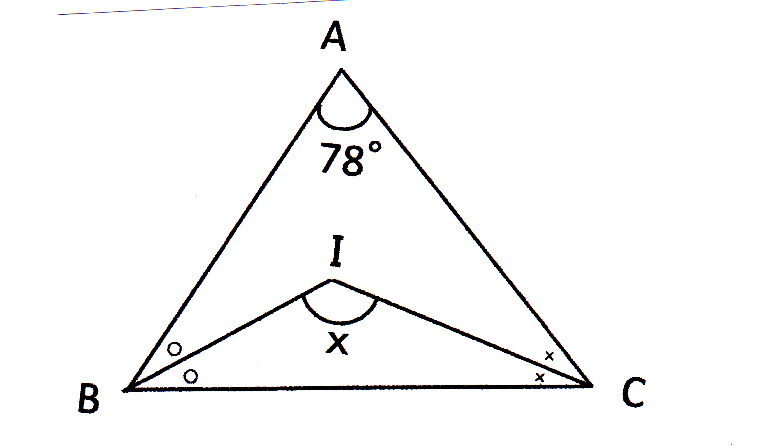
三角形内の角度を求める問題 現役塾講師のわかりやすい中学数学の解き方

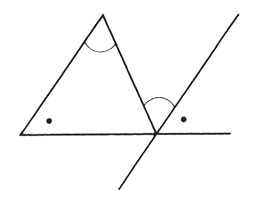
内角の和 算数用語集

 二等辺三角形の角度を求める問題を練習したいですっ★ ってことで、今回の記事では二等辺三角形の角度を求める問題について解説していきます。 角度を求める問題は、図形の性質を覚えてしまえば楽勝！ だから、この記事を通して二等辺三角形教え方1 三角形の3つの角の角度をたすと何度になるか考えさせます。 問い 三角形の紙を用意して、適当に手でちぎって3枚に分け、3つ角をくっつけるとどうなるでしょう？ 実際にやらせたあと、下の動画を、見せます。 直角三角形の角度θの求め方について質問です。 ※三角形の内角は30°60°90°です。 斜辺の長さがわからない時のθの求め方として、｢tanθ=底辺a×高さb｣の公式を使うと思うのですが、この公式ですとθが30°では なく33°になってしまいます。

直角三角形の解法 1

内角の和 算数用語集

 多角形（四角形・五角形・六角形・・・）の内角の和の公式＆問題の解き方 管理人 10月 6, 18 / 11月 18, 18 そしてその中でもさらに多角形の内角の角度に関する問題は頻出されます。 図形の角のまとめ ・三角形の内角の和は 180° ・三角形の外角は「となり合わない2つの角の和と等しい」 ・ 角形の内角の和は 180°×（ −2） この3つは、中学校の数学でも大切な考え方になるので、 しっかり確認しておきましょう！ かずのかず 以上直角三角形 ・直角三角形(底辺と高さ) 直角三角形の底辺と高さから、斜辺と角度と面積を計算します。 ・直角三角形(底辺と斜辺) 直角三角形の底辺と斜辺から、高さと角度と面積を計算します。

正六角形 正6角形 の角度の求め方は 1分でわかる値 内角の和 外角 正多角形の角度の求め方

多角形とは 外角 内角の和 面積 対角線の公式と求め方 受験辞典

三角形の内角の和は180度ですから、「c = 180 a b = 180 35 90 = 55」より、角cの大きさは55度だと分かります。 aとbの求め方 次に、aとbを求めてみましょう。 多角形の内角の和の求め方 角形の内角の和は次のように求めれます。 例 十角形 ⇒ 十二角形 ⇒ なぜ上のような式で求めることができるのか確認しておきましょう。 三角形の内角の和が180°になるというのは知っての通りだね。 これを利用すると 「四角形の内角の和は、三角形の内角の和2つ分と考えて、360度です。」 というまとめになります。 発展（一般化） 適用問題を解いても構いませんが、一般化について考えることができます。 ⑤のやり方は、そのまま五角形の内角の和に応用できますね。

多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学

角度の求め方 算数の教え上手 学びの場 Com

内角の和 180 N 2 外角の和 360 教遊者

接弦定理とは何か 角度別に分かるその証明方法 アタリマエ

多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun

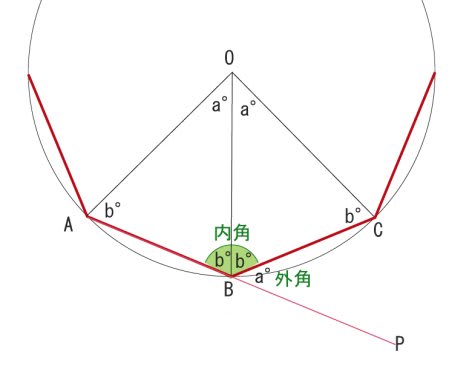
内角 と 外角 って 何だっけ 名寄 算数数学教室より

三角形の角度を求める問題 小学生 中学生の勉強

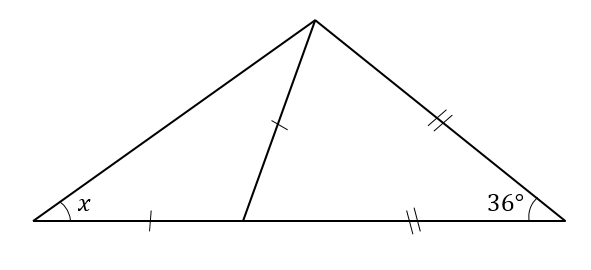
二等辺三角形の角度の求め方を問題を使って徹底解説 数スタ

1

図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に

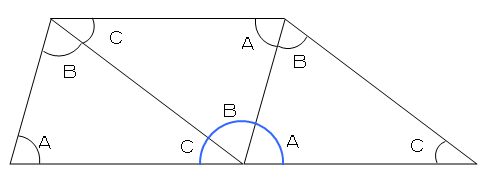
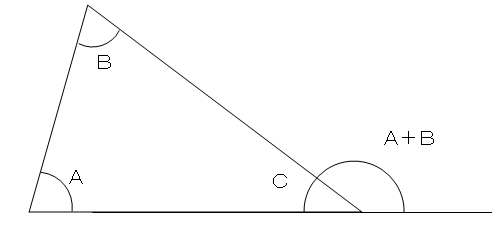
三角形の内角と外角の関係

数学 中2 48 三角形の内角と外角 基本編 Youtube

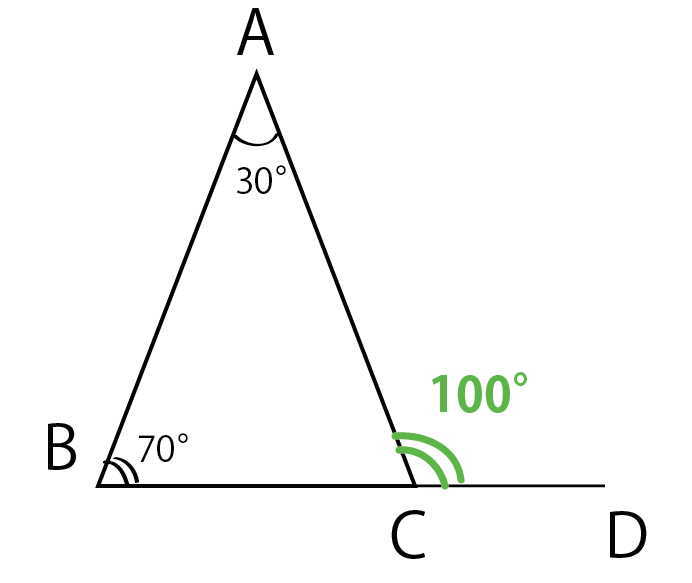
3分でわかる 三角形の外角の定理の証明 Qikeru 学びを楽しくわかりやすく

三角形の内角と外角の性質 教遊者

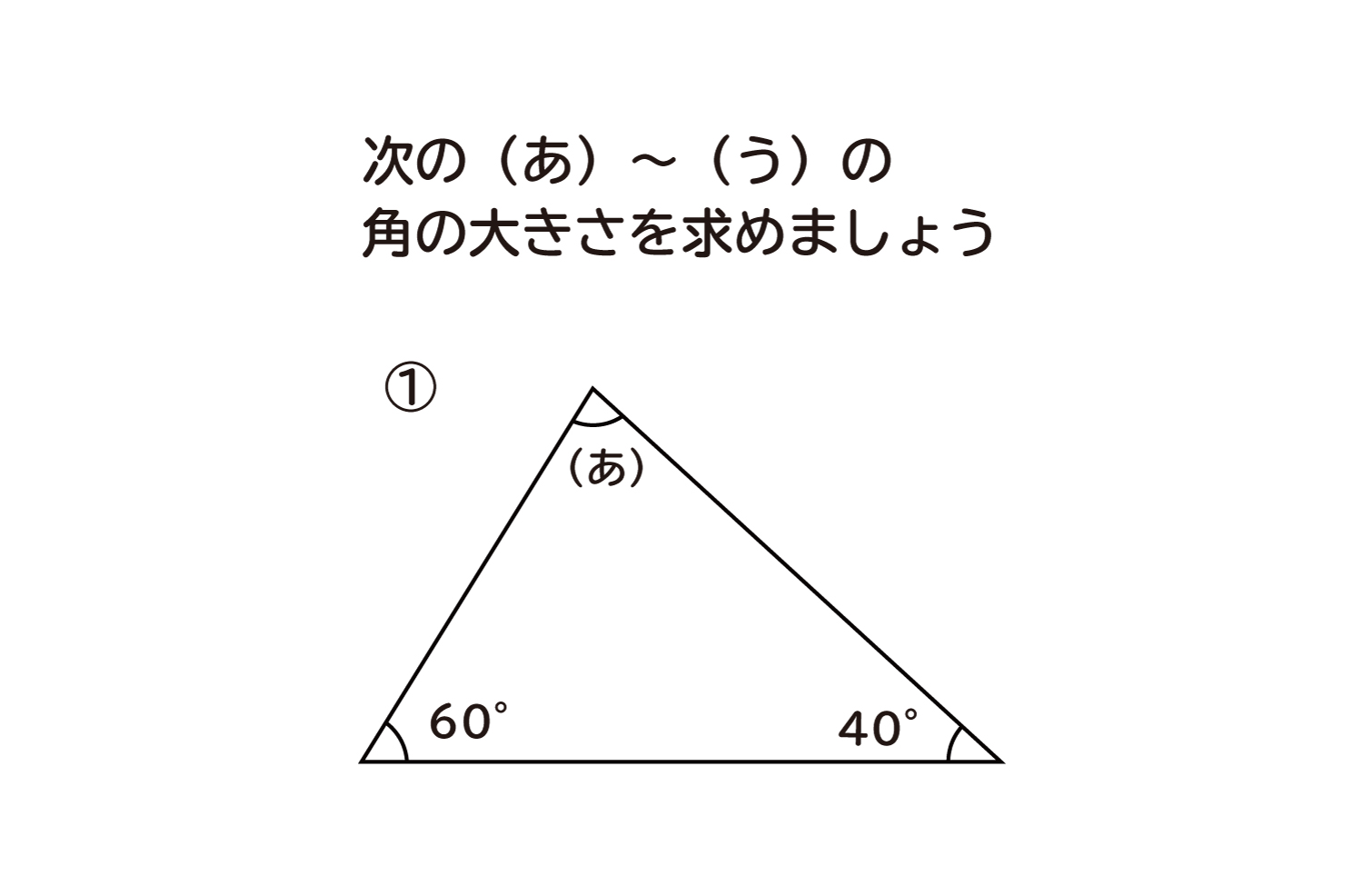
小学5年生 算数 無料問題集 三角形の角の大きさ おかわりドリル

三角形の外角と内角の公式 簡単な問題で 外角の求め方を理解しよう 中学や高校の数学の計算問題

三角形の３辺から角度を計算 高精度計算サイト

課題学習の指導 数学

Math 平行と合同 角の二等分線と角度 働きアリ

三角形の角度を求める問題 小学生 中学生の勉強

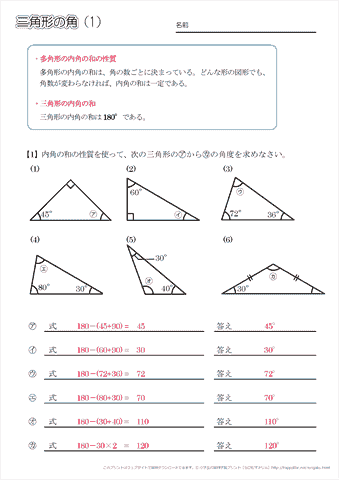
小学５年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生

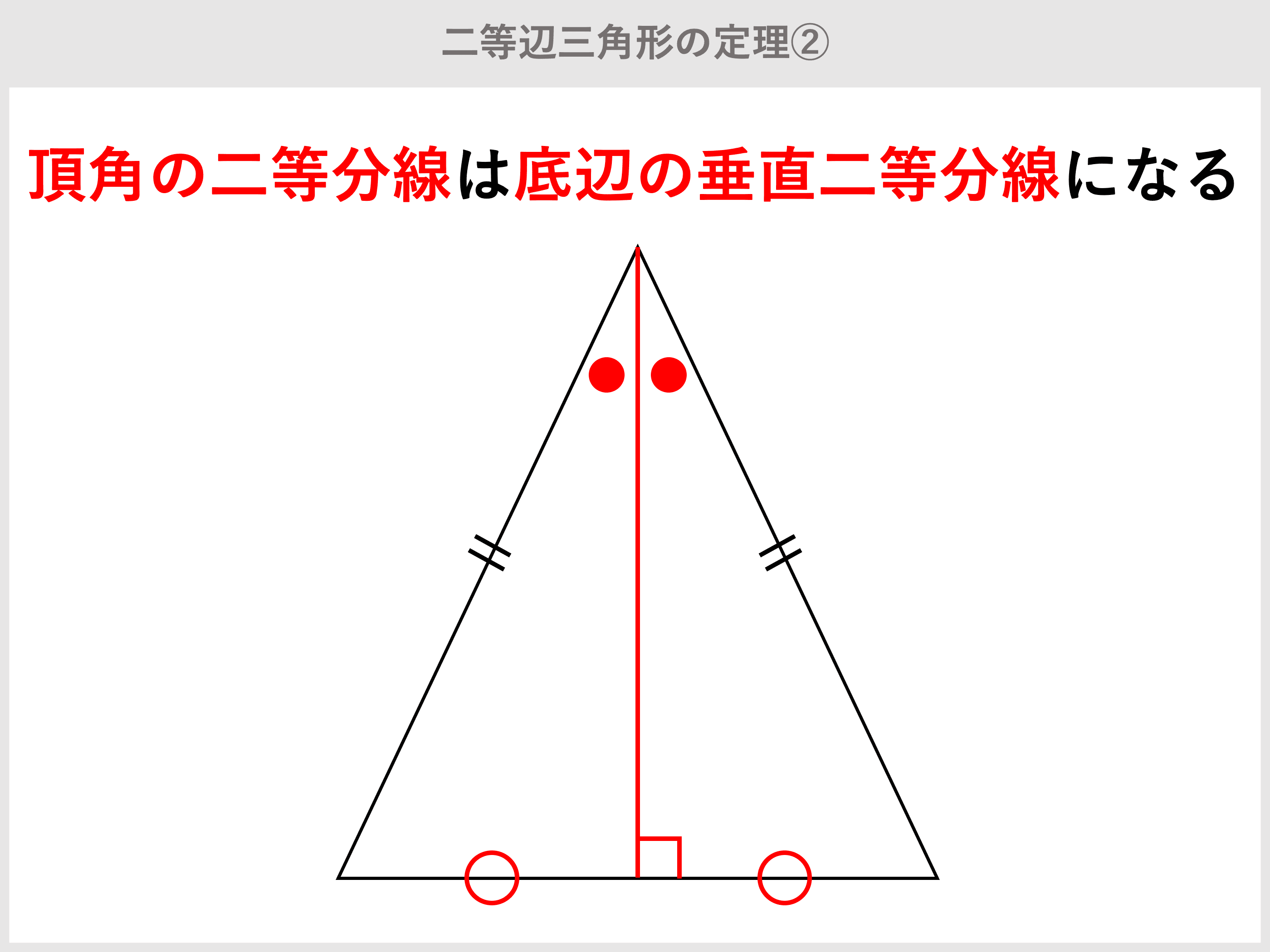
三角角度求め方 Motics

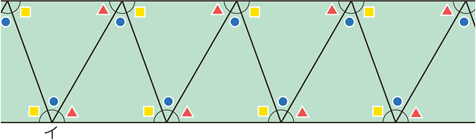
内角の和 算数用語集

外角の求め方 外角の和を使って多角形の角度を求める問題 中学や高校の数学の計算問題

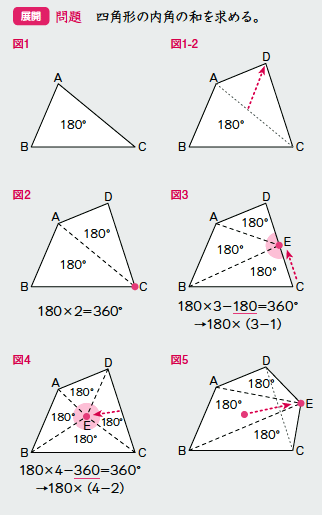
活用 の視点を取り入れた授業例 ２ 図形の性質 四角形の内角の和 ５年生 算数における 活用 とは View21 小学版 09 Vol 2 ベネッセ教育総合研究所

内角と外角 中学受験算数 基本問題 どう解く 中学受験算数

中3数学 円の角度の求め方 練習編 映像授業のtry It トライイット

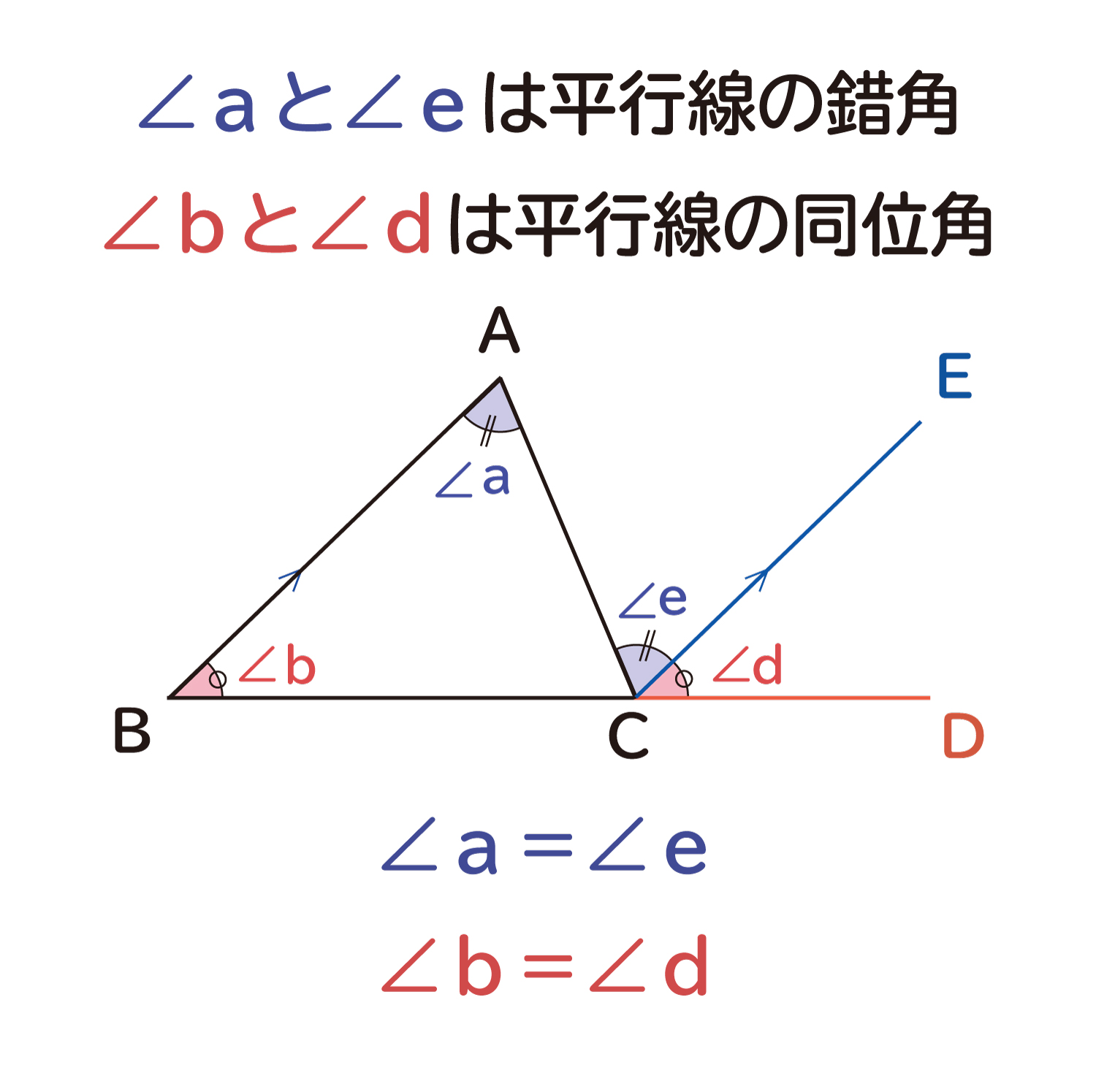
なぜ 三角形の１つの外角は それと隣り合わない２つの内角の和に等しい のか を説明します おかわりドリル

三角形の内角と外角の関係

図形の扉 三角形の外角の定理

タンジェントとは何か 中学生でも分かる三角関数の基礎

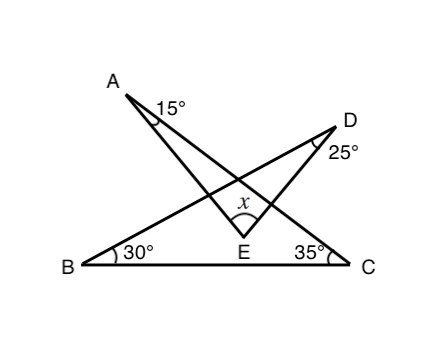
角度を求める問題 スリッパを探そう 苦手な数学を簡単に

中学数学 正三角形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

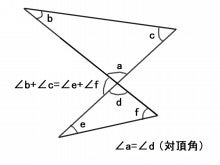
角度の求め方 数学が嫌いなんです

角度の求め方 算数の教え上手 学びの場 Com

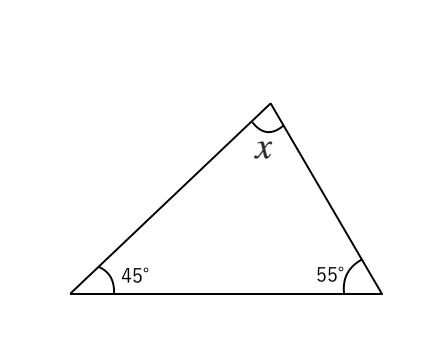
図形の調べ方 三角形についてまるわかり 苦手な数学を簡単に

多角形の内角と外角 思考力を鍛える数学

5年 三角形のふしぎ 算数イメージ動画集 大日本図書

簡単公式 二等辺三角形の角度の2つの求め方 Qikeru 学びを楽しくわかりやすく

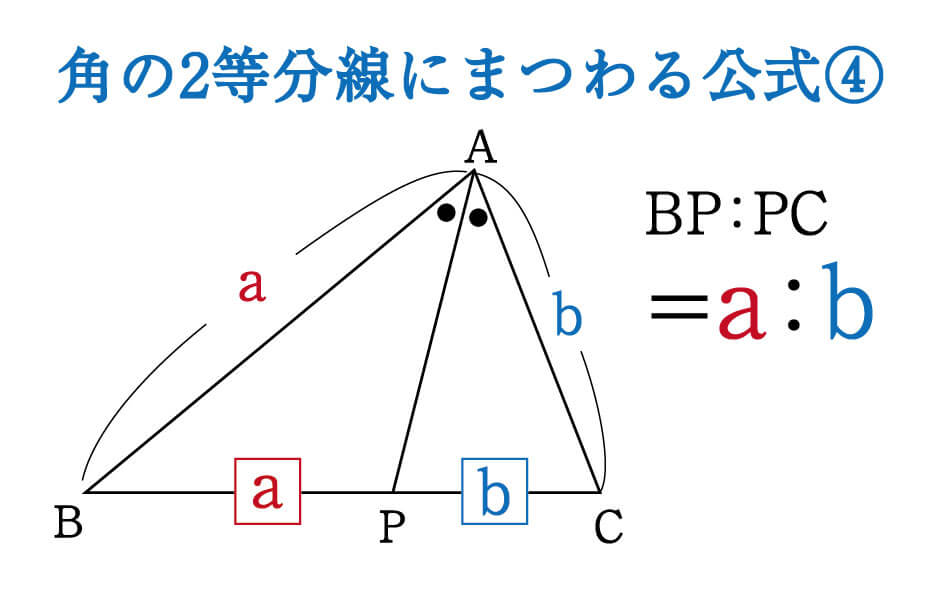
数学 角の二等分線にまつわる絶対に覚えておきたい公式 受験の秒殺テク 8 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

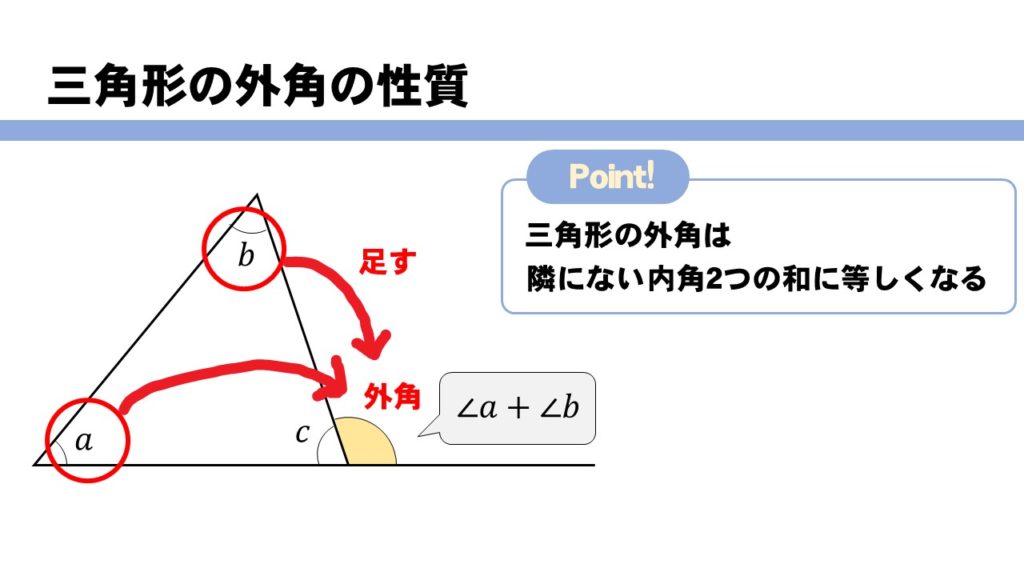
3分なるほど 三角形の内角 外角の性質について解説 数スタ

中2数学 三角形の内角と外角 例題編 映像授業のtry It トライイット

三角形の辺や角が与えられたとき残りの辺や角を求める方法 数学の偏差値を上げて合格を目指す

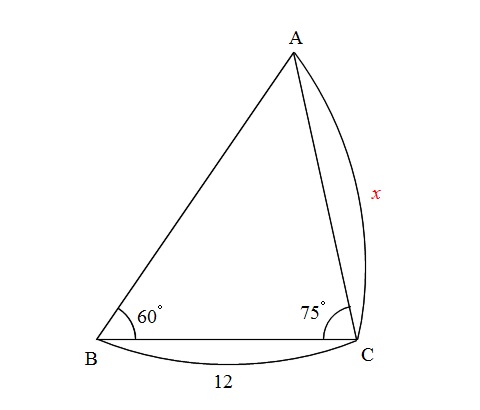
三角形で角度が2つ分かっているのに正弦定理も余弦定理も使えない

小学５年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生

余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ

多角形の内角の和 外角の和の公式 数学fun

正三角形や二等辺三角形の内角 Youtube

1

余弦定理で角度を求める方法 数学の星

三角形の内角の和を帰納的 演繹的に求める方法 算数を究める

高校数学a 三角形の内角 外角の二等分線と辺の比の関係とその証明 受験の月

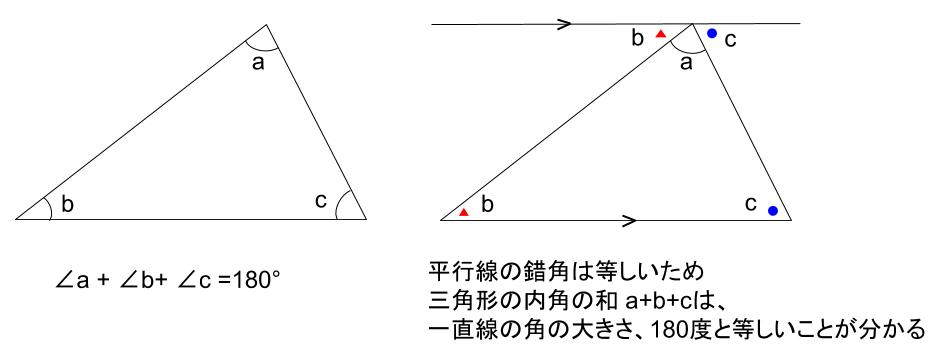
中学数学 三角形の内角 外角 中学数学の無料オンライン学習サイトchu Su

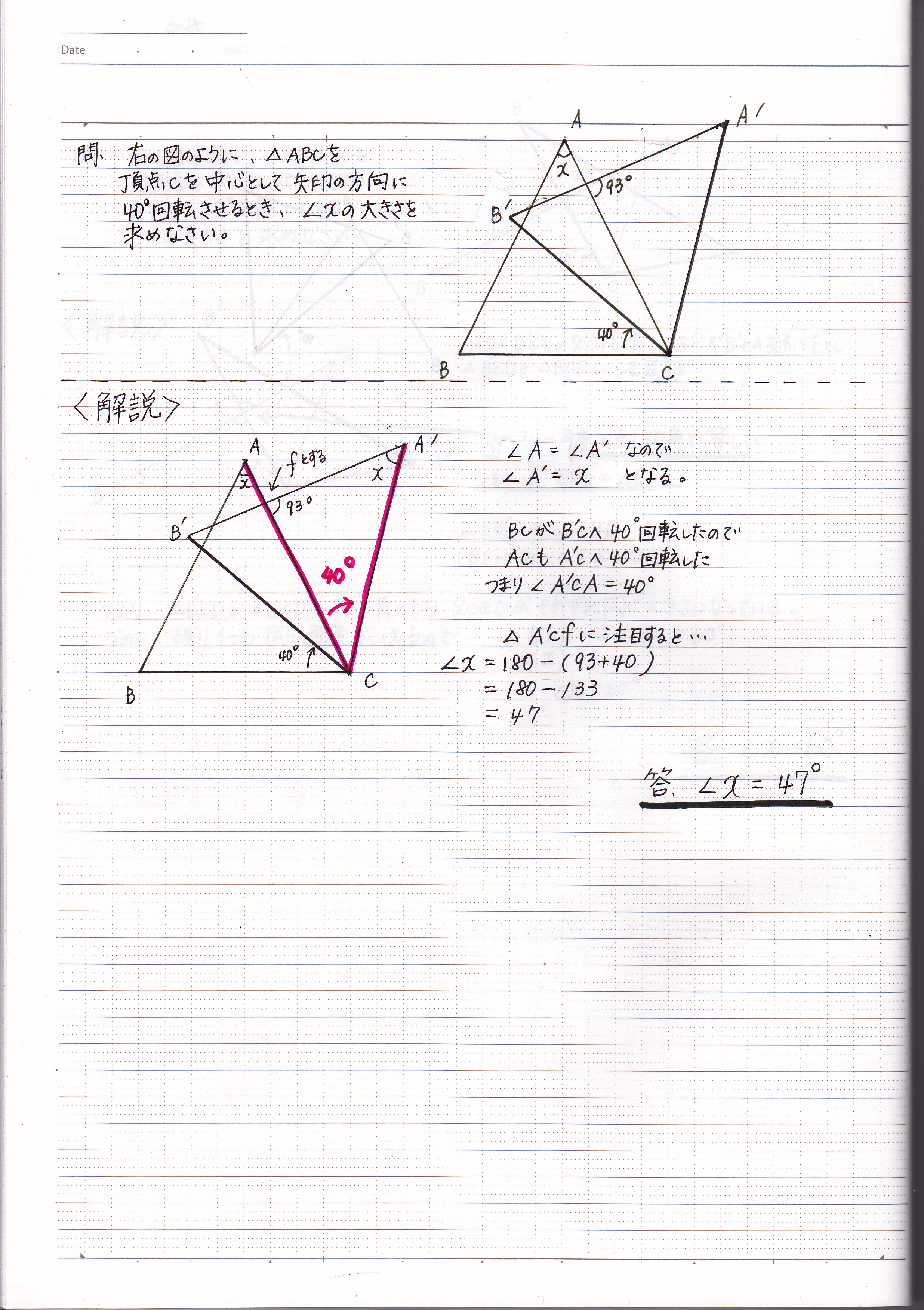
回転する図形の角度の求め方 現役塾講師のわかりやすい中学数学の解き方

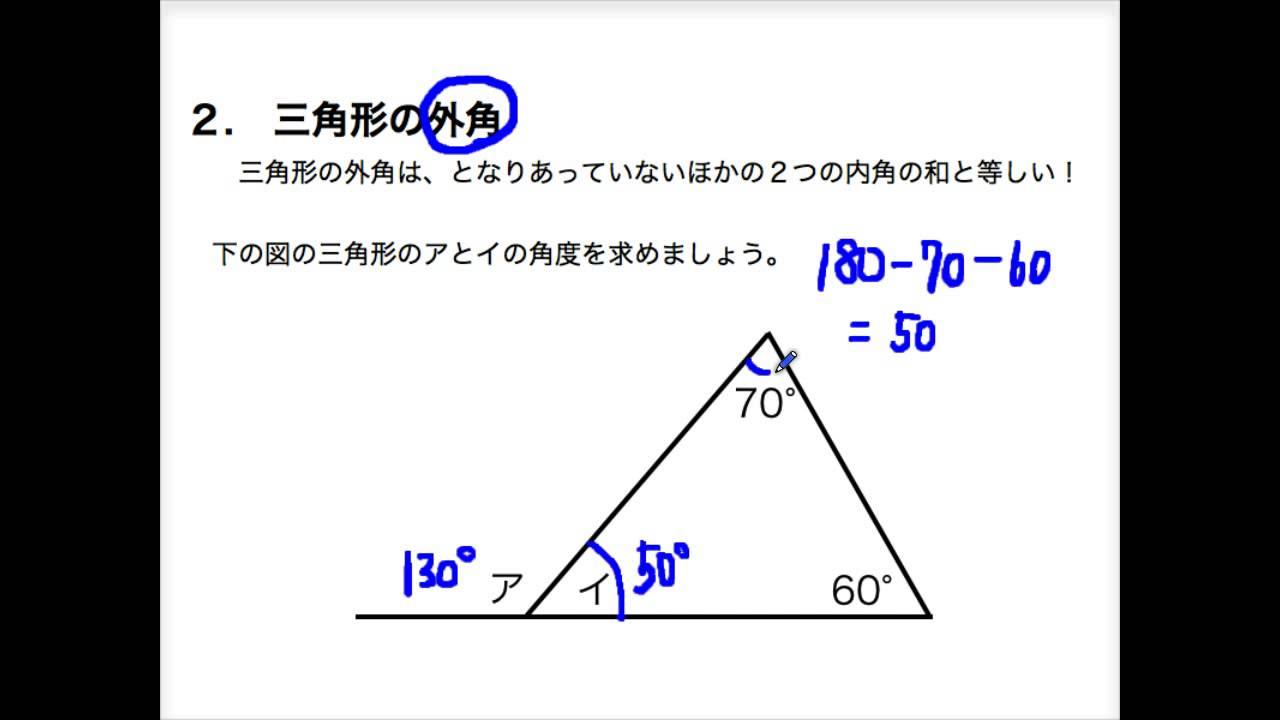
小学校5年 算数 三角形の外角 Youtube

底辺と高さから角度と斜辺を計算 高精度計算サイト

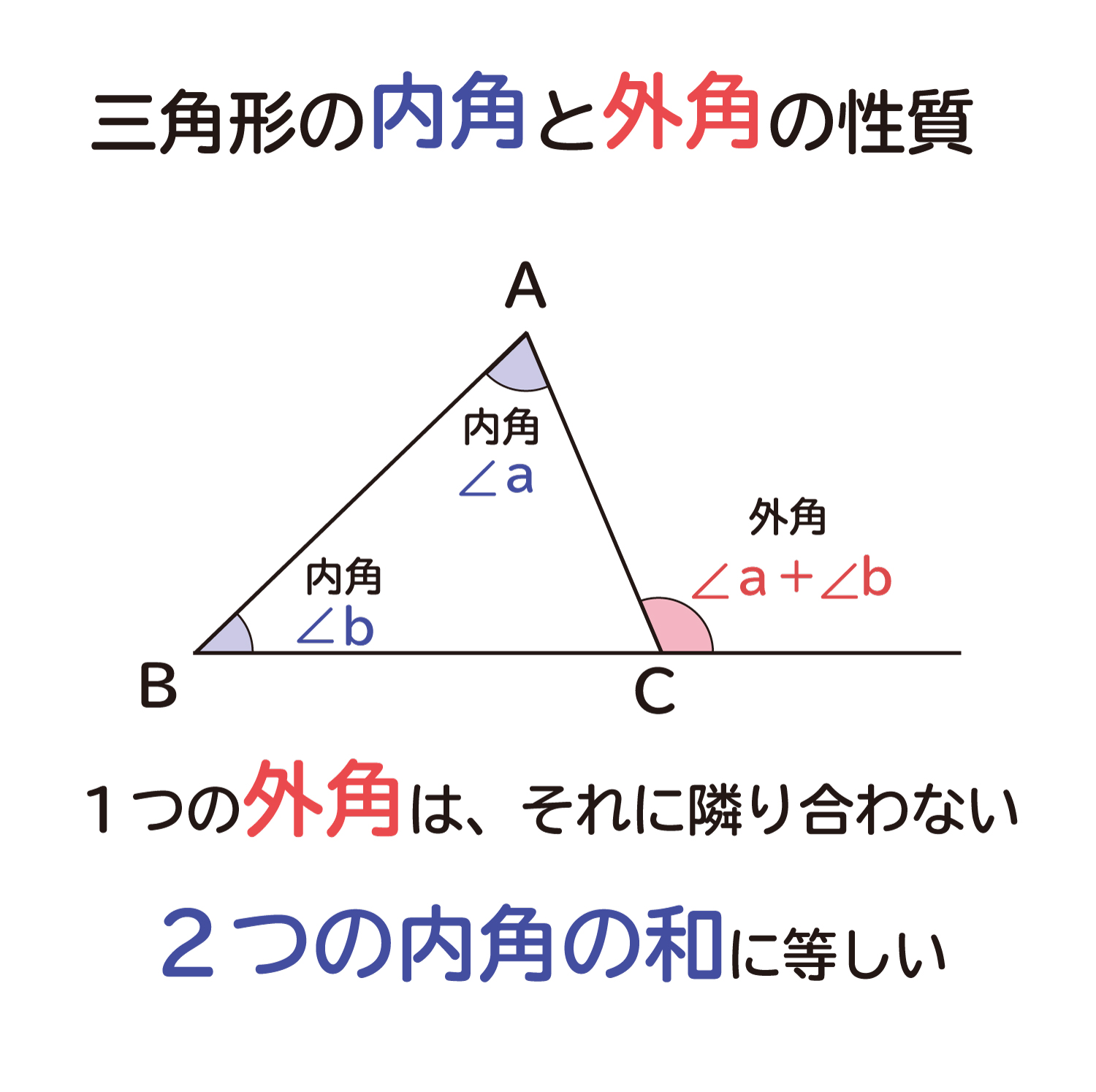
なぜ 三角形の１つの外角は それと隣り合わない２つの内角の和に等しい のか を説明します おかわりドリル

必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ

三角形の角度を求める 思考力を鍛える数学

内角の和から多角形を求める方法と一覧表 具体例で学ぶ数学

小５ 算数 小５ ３１ 三角形の角 Youtube

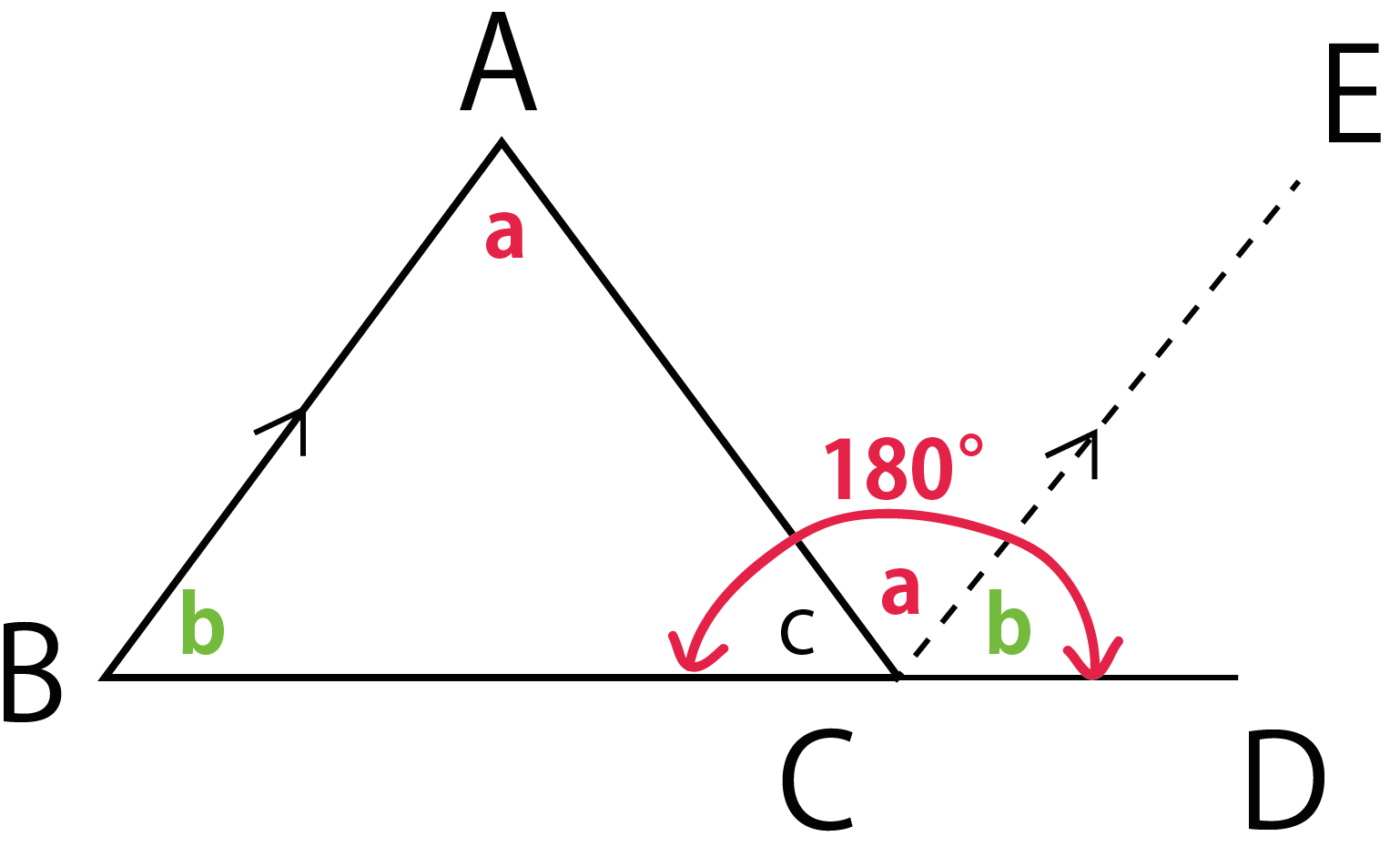
中2数学証明 三角形の内角の和の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ

内接円 内心

中2数学証明 三角形の内角の和の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

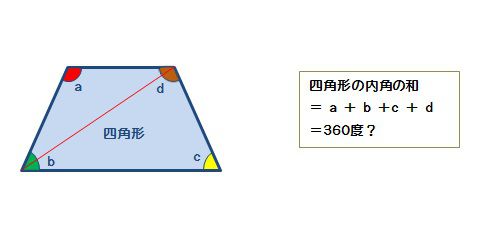
四角形の内角の和 算数の公式覚えてますか

数学 角の二等分線にまつわる絶対に覚えておきたい公式 受験の秒殺テク 8 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

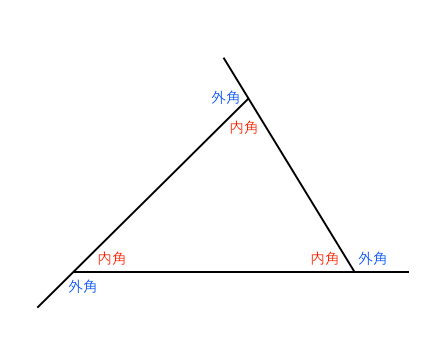
図形の調べ方 外角を求める 苦手な数学を簡単に

なぜ 三角形の 内角の和は180 なのか を説明します おかわりドリル

1

二等辺三角形の角を求める Youtube

三角形の辺から角度を計算 製品設計知識

直角三角形の角度の求め方 教えて下さい 斜辺以外の２辺の長さが分かっ Yahoo 知恵袋

多角形の内角の和 は何度なのか を説明します おかわりドリル

三角形の内角と外角の関係

簡単公式 二等辺三角形の角度の2つの求め方 Qikeru 学びを楽しくわかりやすく

多角形の内角の和 の指導における一考察 子どもの深い学びを実現させるために 授業実践記録 授業支援 サポート資料 数学 中学校 知が啓く 教科書の啓林館

中2数学証明 三角形の内角の和の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

中学数学 内角と外角の関係を利用した問題 実は公式不要 なぜか分かる はかせちゃんの怪しい研究室

二等辺三角形の角度の問題 基礎から応用までパターン別に解説 中学数学 理科の学習まとめサイト

角度の求め方 算数の教え上手 学びの場 Com

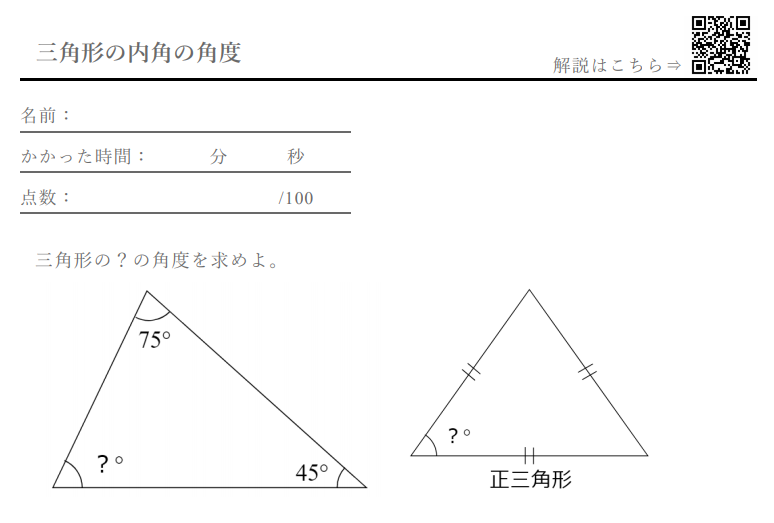
三角形 の内角の角度 計算ドリル 問題集 数学fun

多角形の内角の和の求め方をイチから解説するぞ 中学数学 理科の学習まとめサイト

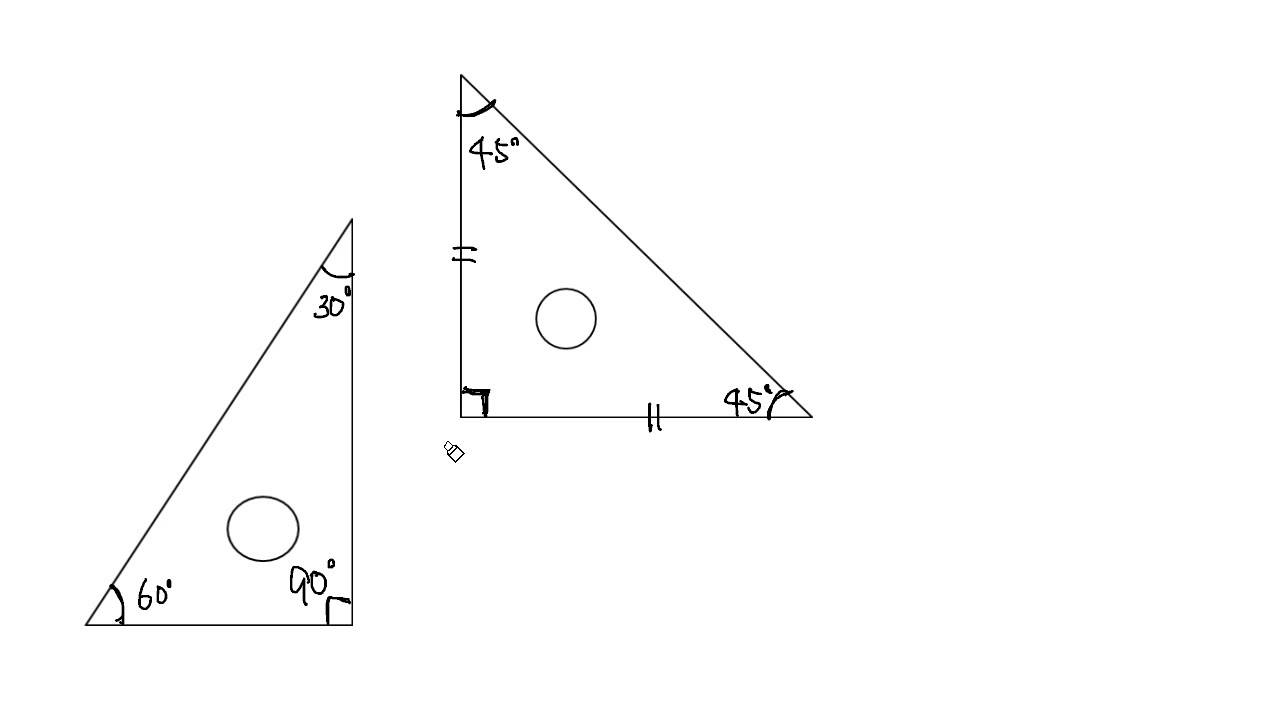
三角形の内角の和 Youtube

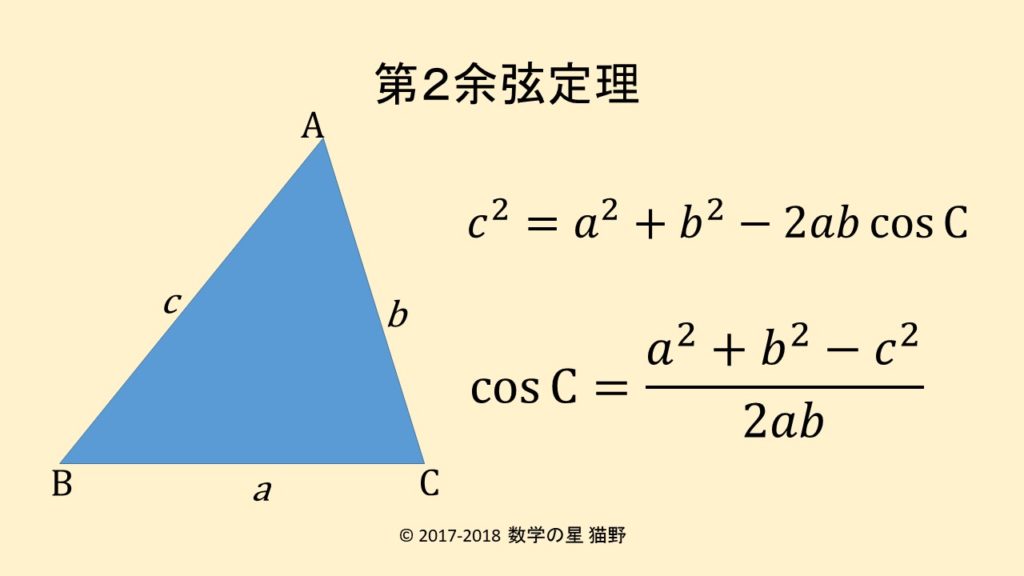
第２余弦定理の公式は辺と角度の関係を簡潔に表す 数学の星

1

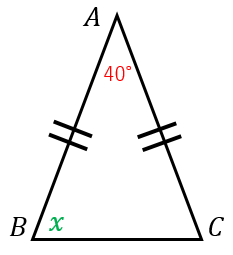
二等辺三角形の角度の求め方と例題 具体例で学ぶ数学

Excel 三角形の角度を底辺や斜辺 高さから求める方法 直角三角形の角度の計算

高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月

直角三角形の解法 1

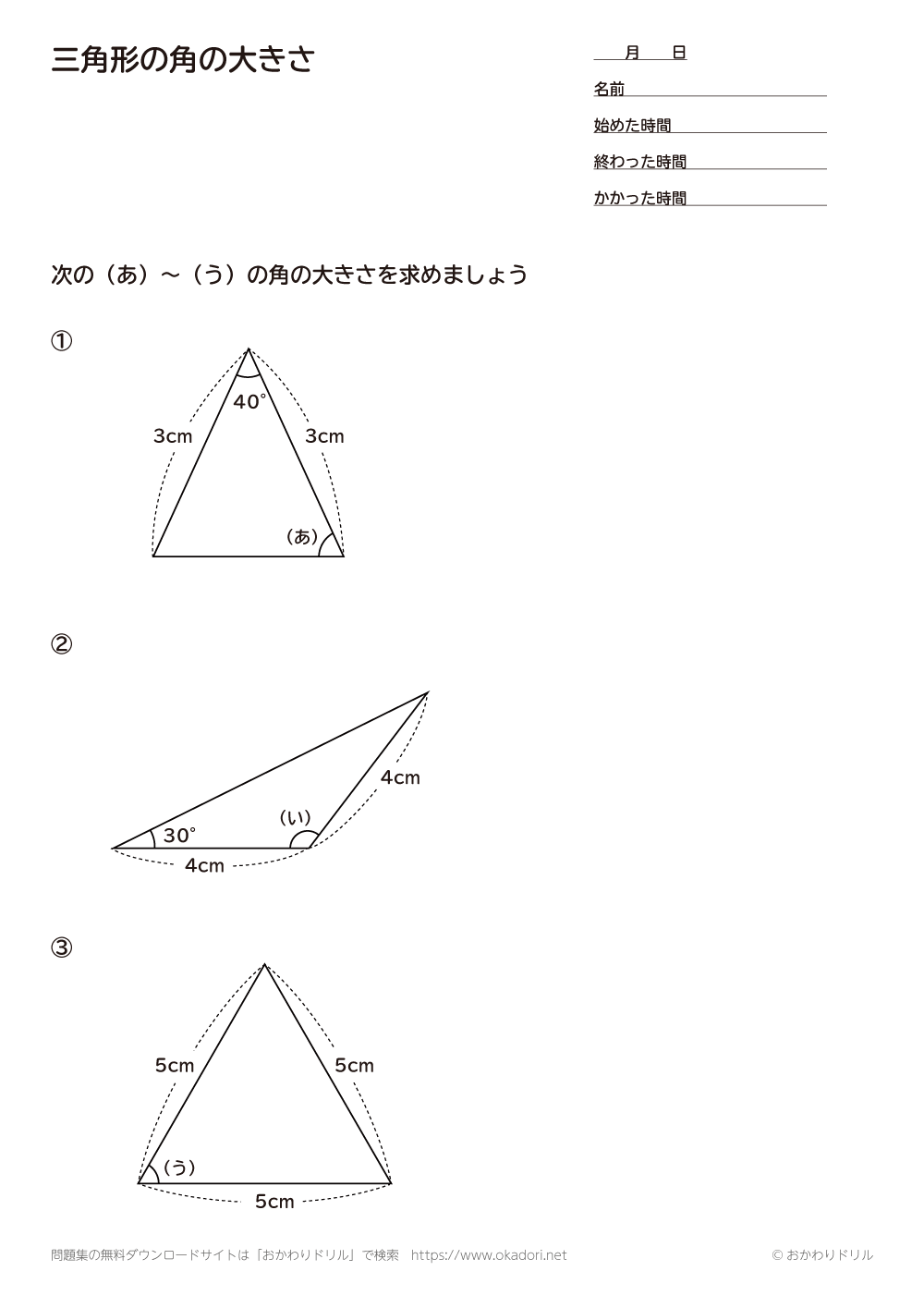
小学5年生 算数 無料問題集 三角形の角の大きさ おかわりドリル

三角形の内角の和は180度って証明できるの 三角形の外角の定理 公式 や問題アリ 遊ぶ数学

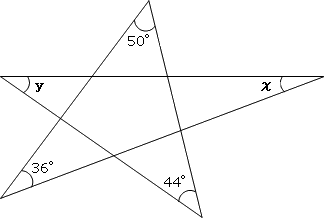
角度の求め方 算数の教え上手 学びの場 Com

外角

角度の計算 裏技まとめ 教遊者

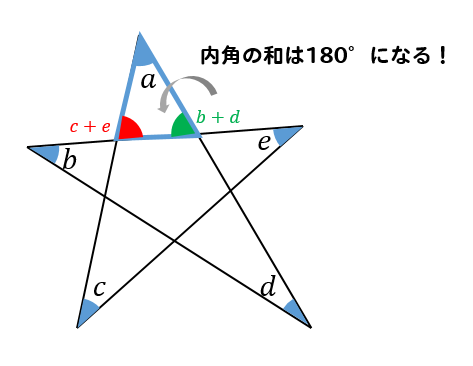
星形の角度 内角の和の求め方を問題解説 数スタ

Incoming Term: 三角形 内角 求め方,